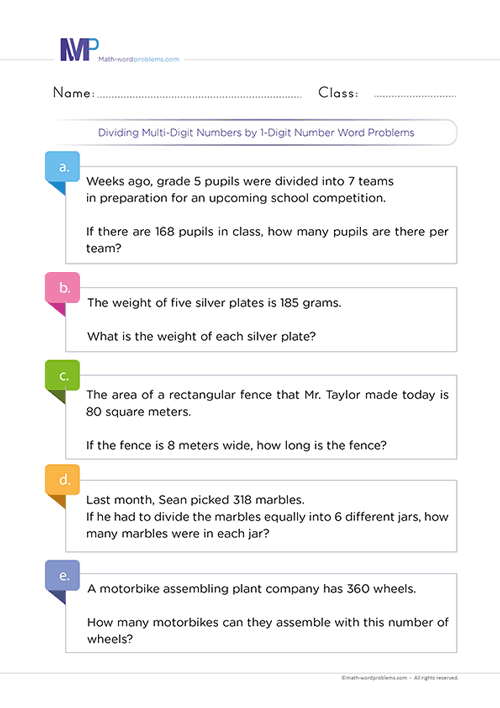
How to solve division of whole numbers ending in zeros word problems
How to solve division of whole numbers ending in zeros word problems
Does your 5th grader know how to solve division of whole numbers ending in zeros word problems efficiently? If no! Then grab this super fun resource with a well-organized and technical step-by-step guide below.
We have observed that kids always face difficulties identifying the operation to solve a particular word problem. To this effect, we will describe the keyword approach in detail, wherein they can use (keywords) to determine the kind of operation they will use at a particular time. However, you will find a lot of division keywords in this resource that will help you solve all division of whole numbers ending in zeros word problems accurately at all times.
On the other hand, we encourage kids to read the problem between the lines first to understand its structure better, rather than solely depending on the keywords. This is because some particular keywords have different meanings in different word problems. So if you don't understand a problem well, such keywords will mislead you.
Steps to solve division of whole numbers ending in zeros word problems
As mentioned above, these steps to solve division of whole numbers ending in zeros word problems will greatly encourage and change the perspective in which grade 5 kids see math word problems, making them great mathematical thinkers.
Learners will develop a deep and special delight for math word problems by the time they master this genuine step-by-step guide. Moreover, this guide will facilitate fifth graders understanding if they continuously practice all the steps in this division of whole numbers ending in word problems resource.
Equally, to build learners' passion for dividing whole numbers ending in zeros word problems, we have added fun examples to engage their minds and familiarise themselves with how the steps work.
Step 1: IDENTIFY THE PROBLEM
To identify the problem, you must read the word problem very carefully to know what the problem wants you to solve.
Also, try to identify important numbers and keywords in the word problem. For instance, If you come across one of the following keywords in a word problem:
- Divide, half, evenly, every, per, parts, out of, quotient of, ratio of, how many in each, equal parts, cut up, average, as much, etc. then it implies that you have to perform a Division Operation.
Note: One key Element for learners to understand is that they should not always rely on keywords alone. That is to say; the same keyword can have different meanings in different word problems.
For this reason, we reiterate on the importance of reading the question very carefully to understand the situation that the word problem is describing, then figure out exactly which operation to use
Step 2: STRATEGIZE OR GATHER RELEVANT INFORMATION
The main question is, "how do I tackle this problem?"
- From the keyword(s) in the word problem, you will know whether you need to perform a Division Operation or any other operation.
- On the other hand, you must not rely only on keywords. Also, try to understand the situation that the problem is describing.
- Next, after knowing which operation you will perform, construct short expressions/sentences to represent the given word problem.
Step 3: CREATE THE EQUATION
Now, write down a numerical expression/ equation representing the information in the word problem.
Step 4: PROVIDE A SOLUTION
From step 3 above, divide the values using the long division method. Strike out the common zeros, if any, before you continue with the long division method. Always remember to add the unit of measurement to your final result.
Step 5: CHECK YOUR WORK
Finally, check if your answer makes sense. For instance, estimate the answer and see if it is close to what you expected. However, if the answer is not what you expected, go back to step one and start all over again.
Examples on how to divide whole numbers ending in zeros word problems.
Example One
Step 1: First, the important numbers here are 10,000 and 2,000. Also, the keyword(s) found in the word problem is "per."
Step 2: Next, how will you solve the problem? The situation the problem is describing and the keyword found in the word problem call for you to perform a division operation.
Now, form short sentences to represent the given word problem.
- Number of binders the bookstore ordered = 10,000.
- Number of binders the company puts per box = 2,000.
- Therefore, the number of boxes the bookstore received = the number of binders ordered ÷ the number of binders the company puts per box.
Step 3:Write down a numerical expression to represent the bolded sentence in step 2 above to solve this word problem:
10,000 ÷ 2,000 = ?
Step 4: From step 3 above, first strike out the common zeros. Then, set up a long division sign, arrange the numbers, and solve using the long division steps. Also, do not forget to include the unit of measurement, if any.
So, the bookstore received 5 boxes of binders.
Step 5: Finally, check out your work, i.e., if the answer makes sense by estimating the numbers and calculating mentally. If the answer is so close to the one you have, then your answer is correct but if the answer is not close to your answer, go back to step 1.
Example Two
Step 1: First, the important numbers here are 2,000 and 20. Also, the keyword(s) found in the word problem is "each."
Step 2: Next, how will you solve the problem? Right now, the situation the problem is describing and the keyword(s) found in the word problem call for you to perform a division operation.
Before proceeding, remember that the problem requires you to provide the final result in liters, not milliliters. So, you will visit your conversion table to solve this problem correctly.
Now, form short sentences to represent the given word problem.
- Quantity of orange juice in the pitcher = 2,000 milliliters.
- Number of children to share the juice = 20.
- Therefore, the milliliters of juice each child will get = the quantity of orange juice in the pitcher ÷ the number of children to share the juice.
Step 3: Write down a numerical expression to represent the bolded statement in step 2 above to solve this word problem:
2,000 ÷ 20 = ?
Step 4: From step 3 above, first strike out the common zeros. Then, set up a long division sign, arrange the numbers on it, and solve using the long division steps. Also, do not forget to include the unit of measurement, if any.
You see that each child will get 100 milliliters of juice.
Let's recall the actual question, "How many liters of juice will each child get?"
So, you have to convert 100mm to liters as shown below:
If 1000mm = 1l,
Then 100mm = (100mm × 1l)/ 1000mm = 0.1l
Therefore, each child will get 0.1 liters of juice.
Step 5:Finally, check out your work, i.e., if the answer makes sense by estimating the numbers and calculating mentally. If the answer is so close to the one you have, then your answer is correct but if the answer is not close to your answer, go back to step 1.