$>$ How do you add four or more one-digit numbers word problems with sums up to 50?

$Lesson summary$

Get more contents on this skill...

How do you add four or more one-digit numbers word problems with sums up to 50? This outstanding resource will provide your 2nd Graders with all the tips and models they need to make the addition of single digit numbers word problems fun and effective.

We encourage your little ones to read, think, identify the problem type, and strategize on carefully solving the problem rather than just recognizing the answer pattern.

Above all, we will design captivating visual representations with an evidenced-based strategy to help kids learn concrete and abstract concepts involving addition enjoyably.

Steps to solve the addition of four or more one-digit numbers word problems with sums up to 50

Hey kids, here are some captivating steps to solve the addition of four or more one-digit numbers word problems with sums up to 50. These steps will help you quickly solve the addition of four or more one-digit numbers with sums up to 50 using stimulating methods of adding, such as thinking strategies, known facts, or the multi-digit addition method.

The visual representation approach will allow kids to solve various simple and complex problems involving adding four or more one-digit numbers with sums of up to 50 accurately. With this in mind, we'll carry you along as we solve the following real-life examples with tips on how to add four or more one-digit with sums up to 50 numbers word problems.

Step 1 IDENTIFY THE PROBLEM

To identify the problem,

First, you must read the problem out loud to yourself to know what the problem is asking,
Then, identify and underline statements that are related,
In addition, when kids read the problem aloud, they are saying and hearing the question. Thus, enabling them to form a clearer picture of the problem in their head before solving it;

Step 2 STRATEGIZE AND DETERMINE THE OPERATIONS

2^nd Graders need to visualize a problem to understand it. As they get to advanced grades, they can start to have a mental representation of the problem in their heads. But at this young age, they should draw a picture explaining what the problem is all about.

i.e., draw a schematic diagram of the problem that will:

Match the representation to the problem,
Accurately translate quantitative detail from the problem to a constructed diagram,
Correctly identify critical points pertinent to solving the problem;

Step 3 DETERMINE THE KEYWORDS

Every word problem has keywords to look out for that tell you what operation to do. As kids practice word problems frequently, finding the keywords will get easier.

Here are some common keywords that you will see when you come across the addition of four or more one-digit numbers word problems with sums up to 50, namely: add, plus, more, total, increase, together/all together, combined, sum, grow, join, both, in all, altogether, how many in all, how much, and, etc.

Note: learners should understand that it would be best not to rely entirely on keywords alone because a particular keyword can have different meanings in different word problems.

In that case, you need to read the question very well to understand the situation the word problem describes. After reading, you will also find out if the problem makes sense first before determining which operation you need to use.

Step 4 STRATEGIZE AND DETERMINE THE OPERATIONS

Now, ask yourself, “What do I need to find in this problem?”

As you know, some word problems are straightforward, but you have to think very well with some.

In this step, you will apply the read-to-understand rule, i.e., you must read the word problem and try to interpret it in your own words.

Furthermore, since each word problem may require a different way to solve, these key points below will enable young math learners to tackle any word problem irrespective of the way the problem is.

First, the keyword(s) in the word problem will help clarify the operation you need to carry out.
However, as mentioned above, using keywords alone to solve word problems has some limits.
1. So, you must first read the word problem to understand its scenario.
2. Reading the problem to understand it will enable you to identify the problem type and relational statement, which, together with the keyword(s) in the problem, will determine the accurate math operation you need.

Step 5 LIST WHAT IS GIVEN

At this point, you should list what you know. Trying to solve the problem without knowing what tools to use will not give an accurate result. For this reason, you need to know all the facts by doing the following:

Now, after knowing which operation you will perform from step 2 above, form short phrases to represent the information given in the word problem,
These short phrases or sentences represent the vital information in the schematic diagram, making it easier to solve the word problem,
Then, you can deduce a solvable maths equation to represent the information given in the phrases you constructed above;

Step 6 SET UP A MATHEMATICAL EQUATION

Here, with the aid of the schematic diagram that you drew in step 2, you will deduce a numerical expression/ mathematical equation that portrays the information given in the word problem (precisely in step 5)

Step 7 SOLVE THE PROBLEM

After writing down the maths equation, you can solve the problem using any addition method of your choice, preferably the column method. Furthermore, always include the unit of measurement in the final result.

Step 8 VERIFY YOUR ANSWER

Finally, check your work to ensure your answer fits the problem asked.

For instance, mathematically, you can check your work by doing the opposite of whatever operation you used in solving the problem asked.

$Find more resources here$

PRACTICE THIS SKILL NOW $Play$

Download worksheet

Additon word problems up to three digits

$Additon word problems up to three digits worksheet$

Print it

Examples of how to add four or more one-digit numbers with sums up to 50 word problems

Example One

A fan of chocolate flavors, bakes 2 Belgian Chocolate Cakes, 3 Nutty Chocolate Cakes, 5 Chocolate Fudge Cakes, and 4 Chocolate Lava Cakes. How many chocolate cakes does he bake in all?

Step 1:Read the problem carefully and underline all the relational statements. Also, try to form a clearer picture of the problem in your head.

Step 2:Now, draw a schematic diagram of the problem:

Let the spheres denote the 2 Belgian Cakes; the squares denote 3 Nutty Cakes, the triangles denote 5 Fudge Cakes, and the circles denote 4 Lave Cakes.

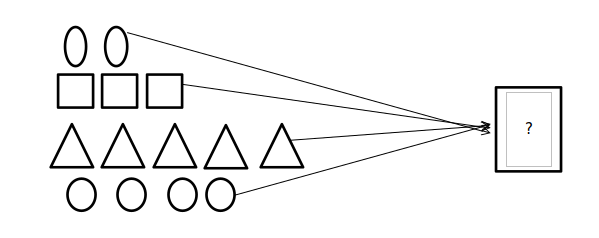
Demo schematic diagram question 2 + 3 + 5 + 4

Step 3:Then, as you reread the problem, the keyword that you’ll come across is “in all”

Step 4: Next, ask yourself, “what do I need to find in this problem?”

First, what is the problem trying to say?

The problem is that a fan of chocolate flavor cakes bakes four different types of chocolate flavor cakes, as illustrated in the schematic diagram above.

The problem requires you to find the number of chocolate cakes he baked.

Now, the question should be: which operation can join four or more similar things into one?

You see that, from the scenario that the problem is describing, from interpreting the problem in your own words, and the keyword found in the word problem, it shows that you have to perform an addition operation.

Step 5: List what is given by constructing short phrases to represent the most vital information in the word problem.

Number of Belgian Chocolate Cakes he baked = 2
Number of Nutty Chocolate Cakes he baked = 3
Number of Chocolate Fudge Cakes he baked = 5
Number of Chocolate Lava Cakes he baked = 4
Therefore, the total number of Chocolate Cakes he baked = the number of Belgian Chocolate Cakes he baked + the number of Nutty Chocolate Cakes he baked + the number of Chocolate Fudge Cakes he baked + the number of Chocolate Lava Cakes he baked.

Step 6:From step 5 above, and with the aid of the schematic diagram in step 2, write a solvable maths equation to represent the bolded statement to solve this problem.

→ 2 + 3 + 5 + 4 =?

Step 7:From step 6 above, stack the values in the equation you formed so their place values line up. Then, add the values using any method, preferably column addition.

You can use the schematic diagram you drew in step 2 above by counting all the objects you drew. The total number of objects will be the final answer.

Also, always add the unit of measurement to the final result.

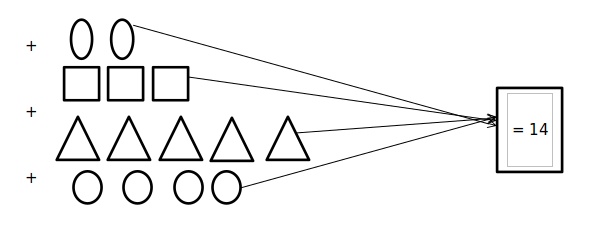
So there are 14 notebooks in her bag.

Step 8: Finally, check your work to ensure your answer fits the problem asked.

For example, mathematically, you can check your work by doing the opposite of whatever operation you used in solving the problem asked.

The opposite of an addition operation is a subtraction operation.

So, if you take away 2, 3, and 5 from 14, will you have 4?

If your answer is “Yes,” then you are right, but if your answer is “No,” go back to step 1 and start again

Do this by striking out 3, 2, and then 5 objects from the total number of 14 objects in the schematic diagram you drew in step 2.

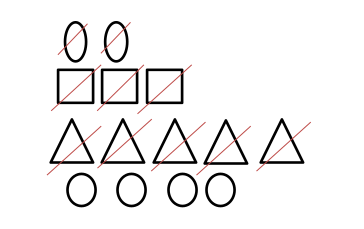
You see that after striking out 3, 2, and then 5 objects, 4 circles remain. So your final answer in step 7 above is correct.

Example One

A breeder has 9 chicken eggs, 7 cane eggs, 3 turkey eggs, and 4 geese eggs. How many eggs does he have?

Step 1:Read the problem aloud and underline all the relational statements. Also, try to form a clearer picture of the problem in your head.

Step 2:Now, draw a schematic diagram of the problem:

Let the black ellipse stands for 9 chicken eggs, the blue ellipse stands for 7 cane eggs, the red ellipse stands for 3 turkey eggs, and the white ellipse stands for 4 geese eggs.

Demo schematic diagram question 9 + 7 + 3 + 4

Step 3:Then, as you reread the problem, the keyword that you’ll find in the problem is “how many”

Step 4: Next, ask yourself, “what do I need to find in this problem?”

First, retell the problem in your own words.

The problem is trying to tell you a breeder has a certain number of different kinds of bird eggs, as illustrated in the schematic diagram above.

The problem wants you to find the number of eggs that he has.

Now, the question should be: which operation can join four or more similar things into one?

Step 5: List what is given by constructing short phrases to represent the most vital information in the word problem.

Number of chicken eggs he has = 9
Number of cane eggs he has = 7
Number of turkey eggs he has = 3
Number of geese eggs he has = 4
Therefore, the total number of eggs he has = the number of chicken eggs + the number of cane eggs + the number of turkey eggs + the number of geese eggs.

Step 6: From step 5 above, and with the aid of the schematic diagram in step 2, write a solvable maths equation to represent the bolded statement to solve the problem.

→ 9 + 7 + 3 + 4 = ?

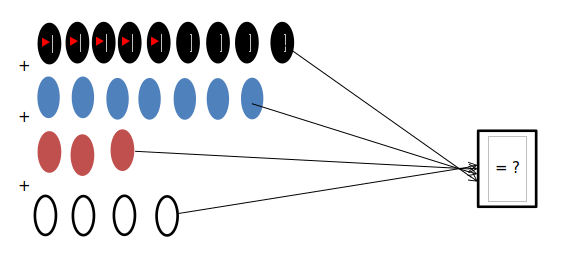
Step 7:From step 6 above, stack the values in the equation you formed, so their place values line up. Then, add the values using any method, preferably column addition.

You can use the schematic diagram you drew in step 2 above by counting all the objects you drew. The total number of objects will be the final answer.

Also, always add the unit of measurement to the final result.

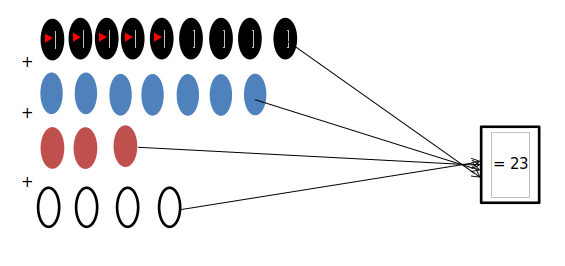
So he has 23 eggs.

Step 8: Finally, check your work to ensure your answer fits the problem asked.

For instance, mathematically, you can check your work by doing the opposite of whatever operation you used in solving the problem asked.

The opposite of an addition operation is a subtraction operation.

So, if you take away 4, 3, and 7 from 23, will you have 9?

If your answer is “Yes,” then you are right, but if your answer is “No,” go back to step 1 and start again

Do this by striking out 4, 3, and then 7 ellipses from the total number of 23 ellipses in the schematic diagram you drew in step 2.

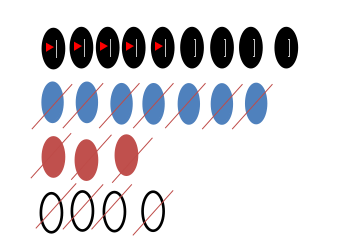
You see that after striking out 4, 3, and then 7 ellipses, 9 ellipses remain. So your final answer in step 7 above is correct.

$>$ How do you add four or more one-digit numbers word problems with sums up to 50?

Get more contents on this skill...