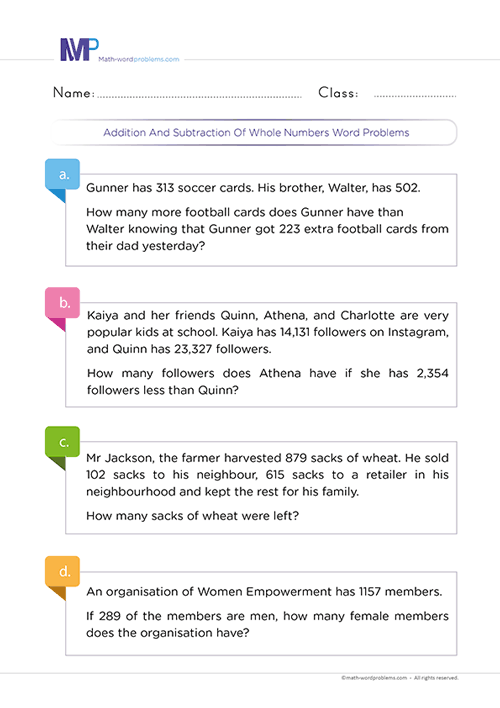
How to solve addition and subtraction of fractions with like denominators word problems
How to solve addition and subtraction of fractions with like denominators word problems
Let’s find out how to solve addition and subtraction of fractions with like denominators word problems by carefully going through this fantastic resource.
We will teach 5th graders a systematic way of solving different problem statements and connecting the mental representation of word problems by converting what they have understood to math equations.
In addition, this motivating step-by-step process of adding and subtracting fractions with like denominators will excite your children to solve any word problems involving fractions with like denominators.
Steps that go into addition and subtraction of fractions with like denominators word problems
Here are the thrilling steps that go into addition and subtraction of fractions with like denominators word problems. These steps will elevate your 5th graders’ minds and prepare them to handle all and any challenges that involve addition and subtraction of fractions with like denominators word problems always pose.
Also, since working with fractions is part of everyday life, we have below some straightforward real-life examples to demonstrate how incredible these steps work.
Step 1: IDENTIFY THE PROBLEM:
To identify the problem, look for the most important parts of the problem. For instance, figure out important fractions and keywords in the word problem. Then, use these keywords to identify whether the problem involves an addition or a subtraction operation.
- The keywords that you’ll likely see when you come across addition of fractions with like denominators word problems are:- add, plus, more, total, in total, increase, together, Altogether, combined, sum, grow, join, both, in all, and, how many in all, how much, etc.
- Also, the keywords that you’ll see when you come across subtraction of fractions with like denominators word problems are: - less, less than, excluding, minus, take away, left, decrease, difference, fewer, deduct, remain, change, how many more, left over, less than, how much longer/shorter, fewer than, discount, etc.
Note: One key Element for learners to understand is that they should not always rely on keywords alone. That is to say; the same keyword can have different meanings in different word problems.
For this reason, we reiterate on the importance of reading the question very carefully to understand the situation that the word problem is describing, then figure out exactly which operation to use
Step 2: STRATEGIZE OR GATHER RELEVANT INFORMATION:
How will you solve or tackle the problem?
Note that each word problem may require a different format, but these vital key points below will help kids conveniently solve any format.
- You will know from the keyword(s) in the word problem if you need to add or subtract or perform any other operation.
- Secondly, you must not rely on keywords alone. Instead, try to understand the situation that the problem is describing.
- Thirdly, when adding and subtracting fractions, all fractions must have the same denominators. So, since you are already dealing with fractions with like denominators here, you are good to go.
- Finally, after knowing which operation you will perform, construct short expressions/sentences to represent the given word problem.
Step 3: CREATE THE EQUATION:
Now, you must write down a numerical equation representing the information in the word problem.
Step 4: PROVIDE A SOLUTION:
From step 3 above, add or subtract the fractions by adding or subtracting the numerators together while leaving the denominator the same. Also, simplify the fraction if possible. Another critical thing to remember is always to add the measurement unit to the final answer.
Step 5: CHECK YOUR WORK:
In conclusion, ask yourself this question. “Does my answer make sense?” If “YES,” you are done. If “NO,” go back to step 1 and start all over again.
Examples on how to perform addition and subtraction of fractions with like denominators
Example one: Here is how to subtract fractions with like denominators.
Step 1:After reading the question discretely, the important fractions that you’ll come across are
Step 2:How will you solve the problem? From the problem description and the keyword “how much more,” it is clear that the question asks to find the difference between the given fractions. Hence, this is a subtraction operation.
We have to construct short sentences to represent the given word problem.
- Fraction of the charity package that was distributed yesterday =
- Fraction of the charity package that was distributed today =
- Therefore, the fraction of more charity packages distributed yesterday than today = fraction of the charity package that was distributed yesterday - fraction of the charity package that was distributed today.
Step 3: Now, write down a numerical equation to represent the bolded statement in step 2 above to solve the problem:
Step 4: Since the denominators are the same, add the numerators and leave the denominators the same. Also, simplify the fractions if possible. Equally, remember to include the unit of measurement in your final answer.
(Since the denominators are the same, just subtract the numerators and leave the denominators the same)
So,
Step 5:Check out your work by interpreting the answer in the context of the problem. If the interpretation makes sense, then “YES,” you are done. If “NO,” go back to step 1 and start all over again.
Example two: how to add fractions with like denominators word problems
Step 1: The important fractions here are
Step 2: How will you solve the problem? Now, the scenario that the problem presents and from the keyword found in the word problem, it is clear that the question asks to find the sum of the given fractions. Hence, this is an addition operation.
Now, we have to Construct short sentences to represent the given word problem.
- Fraction of the charity package that was distributed yesterday =
- Fraction of the charity package distributed today =
- Therefore, the fraction of the charity package distributed yesterday and today altogether = fraction of the charity package that was distributed yesterday + fraction of the charity package distributed today.
Step 3:Now, write down a numerical equation to represent the sentence bolded in step 2 above to proceed with the solution to this problem:
Step 4: Since the denominators are the same, add the numerators and leave the denominators the same. Also, simplify the fractions if possible. Equally, remember to include the unit of measurement in your final answer.
(Since the denominators are the same, just add the numerators and leave the denominators the same)
So,
Step 5:Check out your work by interpreting the answer in the context of the problem. If the interpretation makes sense, then “YES,” you are done. If “NO,” go back to step 1 and start all over again.