Exponents and square roots worksheets Grade 6
Exponents and square roots worksheets Grade 6

- INTRODUCTION
- Download worksheets
- Related Contents
- Why do we practice exponents and square roots worksheets Gra...
Get more contents on Square roots and exponents activities with answers for grade 6...
Are you ready to have fun and explore the world of exponents and square roots worksheets Grade 6? In this resource, you will practice and learn how to use the power rule to simplify expressions and exponents and find the square root of a number using repeated multiplication. For instance, the expression 53 means 5 x 5 x 5. In this example, the exponent (power) is the smaller number (3) on top, while the base is 5, i.e., the number below.
Unlike exponents, which are a way of writing repeated multiplication, square roots are the opposite. They tell you what number multiplied by itself gives you another number. For example, the square root of 16 is 4 because 4 x 4 is 16.
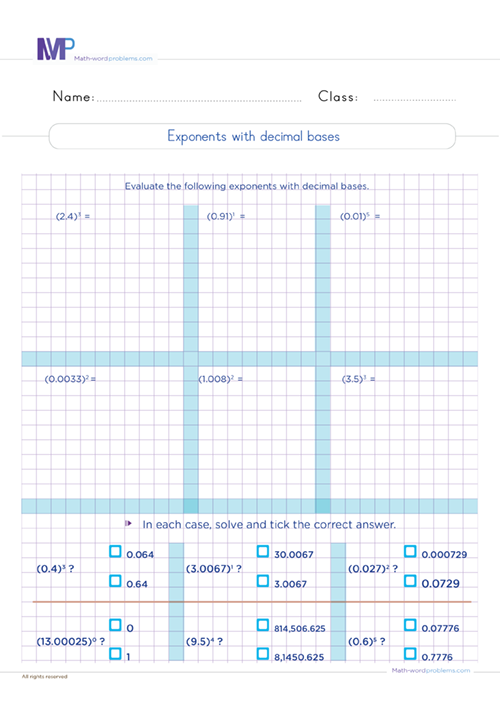
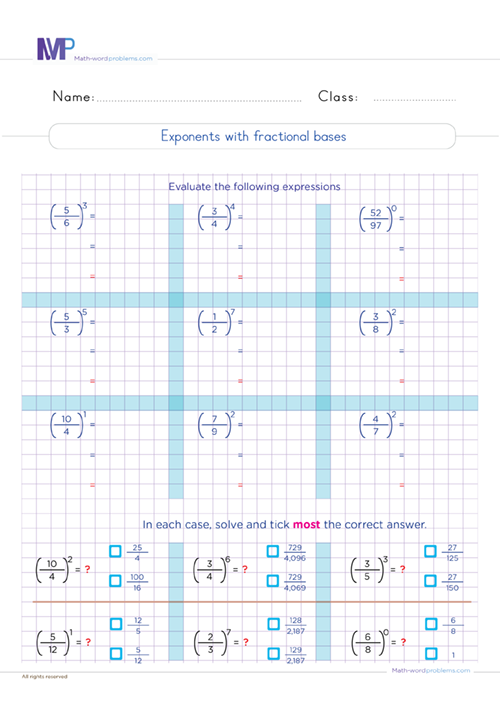
With an understanding of the meaning of exponents and square roots, get ready to solve plenty of math exercises related to exponents and square roots, some of which include; writing multiplication expressions using exponents, evaluating exponents, finding missing exponents or base, exponents with fractional and decimal bases, etc.
Powers and roots worksheets with answers for Grade 6
Help your 6th graders find good quality powers and roots worksheets with answers for Grade 6 only in this resource. We will provide a wide range of well-organized questions to enhance kids' mastery of power rules and how to simplify square roots. Also, given that square roots are one of the essential concepts in maths, with many applications in geometry, algebra, etc., we have decided to combine fun with learning for quick mastery and a solution and answer sheet where kids can be referenced in case they make a mistake while solving.
However, while we engage in solving these exponents and square roots worksheets Grade 6, let us find out what powers and roots are. As we said earlier, power is the exponent that a variable is raised to. For example, the expression 3² is read as 3 to the power of 2, or 3 squared, which means that the value of 3 is multiplied by itself as many times as the value of the power or exponent.
The square root of a number is the inverse operation of squaring a number. The square of a number is the value obtained when we multiply the number by itself. For example, the square of 5 or 52 = 25. On the other hand, the square root of a number is obtained by finding a number that, when squared, gives the original number. For instance, the square root of 25 is 5.
Why do we practice exponents and square roots worksheets Grade 6
Most kids often ask this question, "why do we practice exponents and square roots worksheets Grade 6". Find answers here.
First, some numbers are usually big, cumbersome, or tedious to read and write. In this case, exponents skills helps us to abbreviate such numbers easily. For instance, 31 billion (31,000,000,000) can be abbreviated as 31 x 109. Our exercise, "write powers of 10 with exponents", will efficiently help you in mastering this skill.
Also, as you evaluate exponents, you'll realize they are appropriate and powerful tools for working with large or small numbers. They help us simplify and communicate these numbers more efficiently and accurately.
Understanding base as a whole number, fractional and decimal bases
Understanding base as a whole number, fractional and decimal bases is vital to efficient solving exponents and square roots worksheets Grade 6. So, right now, we'll explore the concept of base as a whole number, fractional and decimal bases in grade 6. Base is the number of different digits that can be used to write a number in a specific system. For example, in the decimal system that we use every day, the base is 10 because we have 10 digits from 0 to 9. In the binary system, which computers use, the base is 2 because there are only two digits: 0 and 1.
But did you know that base can also be a fraction or a decimal? That's right. We can use fractions or decimals as bases to write numbers differently. For example;
-
if we use base 1/2, we can write the number 1 as (1/2)0 + (1/2)1 = 0.5 + 0.5 = 1.
-
Using base 0.1, we can write 1 as (0.1)-1 + (0.1)0 = 10 + 1 = 11.
As you can see, using different bases can help us understand numbers better and see patterns and relationships that might not be obvious in the decimal system. For example, using base 1/2 can help us understand fractions and decimals better because every fraction or decimal can be written as a sum of powers of 1/2. Using base 0.1 can help us understand place value better because every digit in a number represents a power of 0.1.