Symmetry and transformation worksheets Grade 6

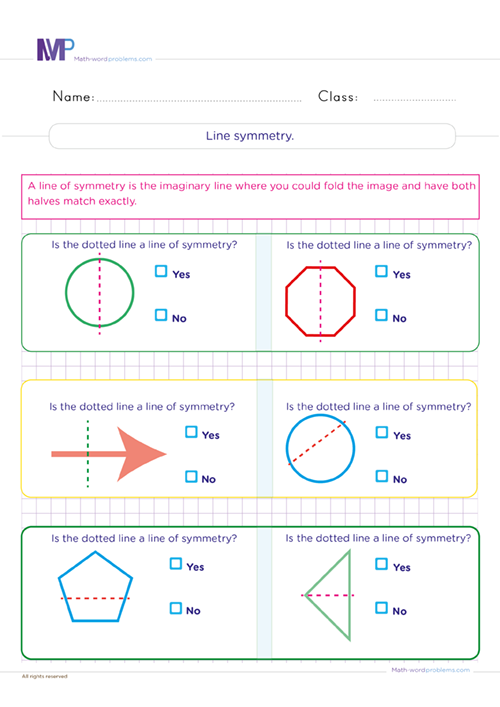
Your 6^th graders will have an exciting experience with our engaging symmetry and transformation worksheets Grade 6, aimed to embed concepts and skills of geometry and spatial reasoning. These worksheets will provide a fun learning experience with practice questions such as drawing lines of symmetry, determining if a shape is symmetric, and reflection and flipping questions. Such exercises are perfect for 6^th grader's mastery of the symmetric concept because a shape is symmetrical only if it can transform (turn, flip, or slide) and remain unchanged, i.e., size, area, angles, and line lengths remain identical.

To better understand the idea of symmetry, kids must remember that a shape or an object has symmetry if it can be divided into two identical pieces. In a symmetrical shape, one half is the mirror image of the other. The imaginary axis or line along which the figure can be folded to obtain the symmetrical halves is called the line of symmetry. We call this line the axis of symmetry or mirror line because it divides the figure symmetrically, and the divided parts look like mirror reflections. Note that a symmetry line can be horizontal, vertical, or diagonal. Thus, we will draw different shapes for kids to identify the lines of symmetry for each shape.

However, constant practice with these unique worksheets will help kids understand the concept better, improve their spatial sense, and thinking ability due to the imagination needed to solve the symmetric exercises. Let's now find out what it means by translation, rotation, and reflection.

Translation, rotation, reflection worksheet 6th grade

Grab the best of quick translation, rotation, reflection worksheets 6th grade, helping to understand the change in position, orientation, or size of a shape.

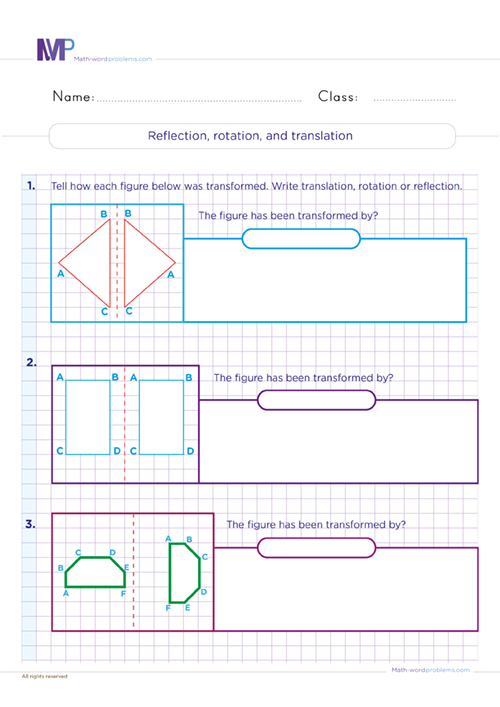
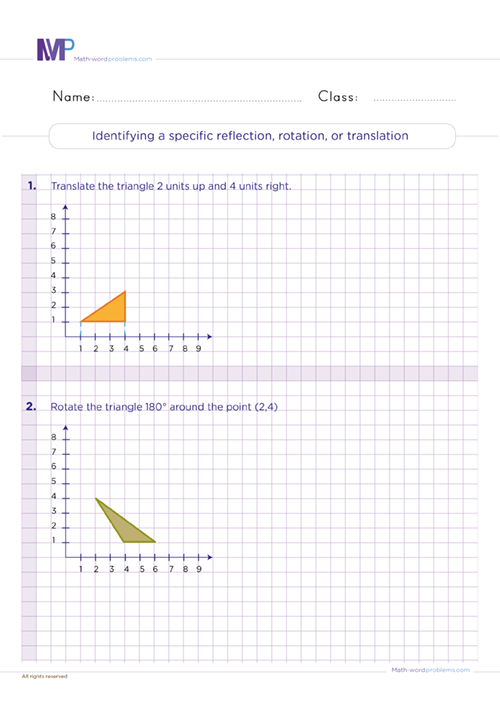
• Translation is when you move a shape up or down or from one side to another. When we translate a shape, each vertex (corners) will move precisely the same way.

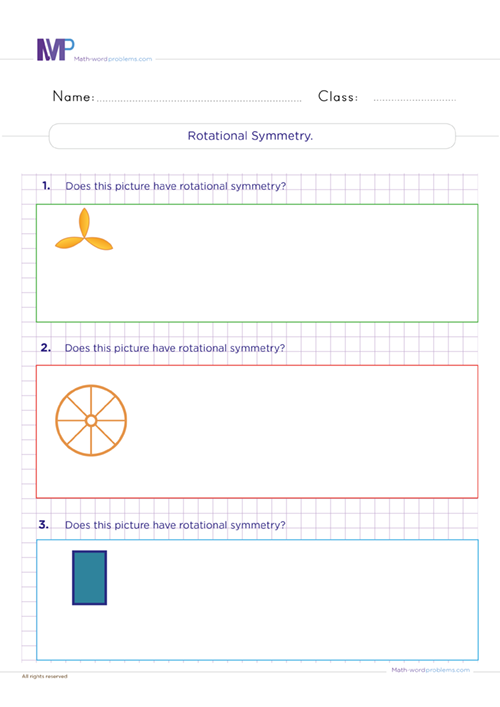
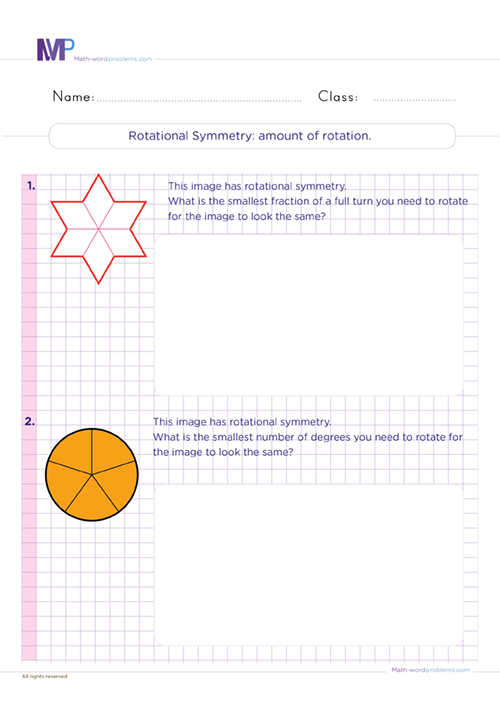
• Rotational symmetry refers to how many times we can fit a shape into itself when we turn it 360 degrees about its center. Many 2D shapes have rotational symmetry because their angles and side lengths are always the same.

• We can refer to reflection symmetry as mirror symmetry reflection. It causes a shape to duplicate itself. For instance, you'll always see your image in a mirror. You and your image appear to be the same distance and angle away from the mirror. This mirror acts as a line of reflection through which your image is copied.

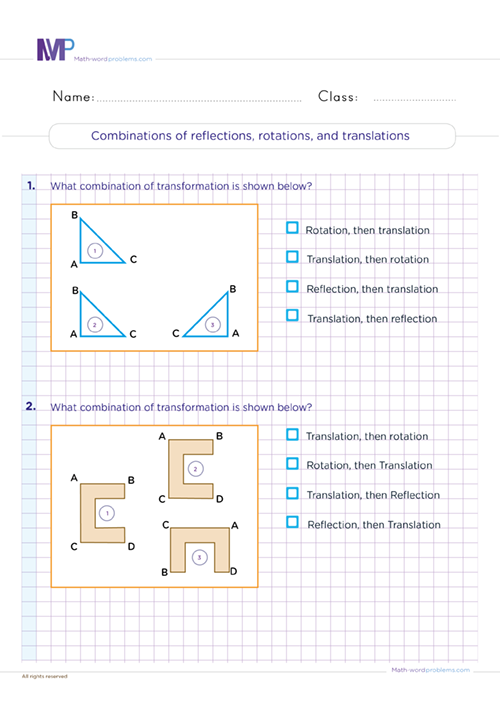
Note that only translation and rotation cause a shape to move from one position to another. With mastery of the above transformation processes, our symmetry and transformation worksheets Grade 6 will provide fantastic skills and methods with different simple shapes on a grid for kids to translate, rotate, or reflect. Then, have them plot the new coordinates on another grid and compare the original and transformed shapes.